논문을 읽을때는 구현이 어려워 보이지는 않았었다. 자세한 구현내용은 깃허브 링크로 대체했는데 모델이 Theano로 구현돼 있었고 논문이 나온 후 GAN의 아키텍처가 많이 발전돼서 정확히 논문 그대로의 예제를 찾기 어려웠다.
그러다 보니 구현 중에 다양한 예제를 참고했으며 이것저것 시도해 보니 데이터셋이 쉬워서 그런지 어떤 방식으로도 생성엔 문제가 없는 것 같다.
Maxout을 사용한 이 레포의 모델을 많이 참고했다.
Generator
class Generator(nn.Module):
def __init__(self, input_dim=100, output_dim = 784):
super(Generator, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.linear_1 = nn.Linear(self.input_dim, 1200)
self.linear_2 = nn.Linear(1200, 1200)
self.linear_3 = nn.Linear(1200, self.output_dim)
def forward(self, x):
x = self.linear_1(x)
x = F.relu(x)
x = self.linear_2(x)
x = F.relu(x)
x = self.linear_3(x)
x = F.relu(x)
return xGenerator쪽에서는 그다지 신경 쓸 부분 없이 100차원 noize vector에서 MNIST의 feature size인 784로 이어지는 Linear 연산을 사용했다.
Discriminator
class Maxout(nn.Module):
def __init__(self, input_dim=784, output_dim=784, k=3):
super(Maxout, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.k = k #[batch, input_dim]
self.linear = nn.Linear(self.input_dim, self.output_dim * k) #[batch, output_dim * k]
def forward(self, x):
self.input_size = x.size()
x = self.linear(x)
x = x.view(-1, self.output_dim, self.k).max(dim=2)[0]
return xclass Discriminator(nn.Module):
def __init__(self, input_dim=784, output_dim = 1):
super(Discriminator, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.max_1 = Maxout(self.input_dim, 240, k=5)
self.drop_1 = nn.Dropout(0.8)
self.max_2 = Maxout(240, 240, 5)
self.linear = nn.Linear(240, 1)
def forward(self, x):
x = self.max_1(x)
x = self.drop_1(x)
x = self.max_2(x)
x = self.linear(x)
x = F.sigmoid(x)
return xDiscriminator는 논문 그대로 Maxout을 사용했는데 Ian goodfellow가 고안한 activation이며 Dropout과 사용할 시 효과가 좋다고 알려져 있다. 최근에는 Linear와 LeakyReLU의 조합을 보통 사용하는 것 같은데 MNIST를 훈련시킬 때는 위의 구조와 큰 차이를 보이진 않았다.
Training

논문에서 제시한 훈련방식은 위와 같은데 BCE loss를 사용하면 D쪽은 구현이 가능하고 Generator쪽도 BCE loss를 사용했다.
mnist_train = datasets.MNIST(
"../Datasets/MNIST_PyTorch/",
train=True,
transform=transforms.ToTensor(),
download=True
)
mnist_loader = DataLoader(
mnist_train,
batch_size=BATCH_SIZE,
shuffle=True,
drop_last=True
)
latent_dim = 100
D = Discriminator().to(device)
G = Generator(latent_dim).to(device)
epochs = 500
criterion = torch.nn.BCELoss()
optimizer_G = torch.optim.Adam(G.parameters(), lr=1e-3)
optimizer_D = torch.optim.Adam(D.parameters(), lr=1e-3)
for epoch in range(epochs):
d_loss = 0.0
g_loss = 0.0
temp1 = 0.0
temp2 = 0.0
real_y = torch.autograd.Variable(torch.ones((BATCH_SIZE, 1)).cuda())
fake_y = torch.autograd.Variable(torch.zeros((BATCH_SIZE, 1)).cuda())
loss = nn.BCELoss()
for i, data in enumerate(mnist_loader):
#Sample minibatch from sample and z&d
real = data[0].view(BATCH_SIZE, -1).to(device)
fake = G(torch.randn(BATCH_SIZE, 1, latent_dim, requires_grad=False).to(device))
loss_real = criterion(D(real), real_y)
loss_fake = criterion(D(fake), fake_y)
#calculate D_loss
optimizer_D.zero_grad()
loss_D = loss_real + loss_fake
loss_D.backward()
optimizer_D.step()
d_loss += loss_D.detach().cpu()
temp1 += loss_real.detach().cpu()
temp2 += loss_fake.detach().cpu()
#Train G
fake = G(torch.randn(BATCH_SIZE, 1, latent_dim, requires_grad=False).to(device))
y = D(fake)
loss_G = criterion(y, real_y)
optimizer_G.zero_grad()
loss_G.backward()
optimizer_G.step()
g_loss += loss_G.detach().cpu()
d_loss = d_loss / len(mnist_loader)
g_loss = g_loss / len(mnist_loader)
print(f"[Epoch {epoch} losses] D loss: {d_loss}, G loss: {g_loss}")
print(f"[Epoch {epoch} losses] D real: {temp1/ len(mnist_loader)}, D fake: {temp2/ len(mnist_loader)}")
print()
500에폭정도 학습시켰을때 아래와 같은 결과물이 나왔는데 논문보다는 선명도가 조금 떨어지는 느낌이다.

GAN loss
구현은 어려운 편이 아니었는데 하고 나서 의문점이 하나들었다.

GAN의 loss를 구하라고 하면 대게 위의 식을 떠올릴텐데 훈련 과정에는 아래와 같은 식을 사용했다.

구현할때는 넘어갔는데 애매한 부분 중 하나가 Generator를 학습할때 BCE loss를 사용한 점이다. 논문의 Training 부분에 쓰여있는 Generator식에는 BCE loss로 표기된 것이 아닌것 같아 값을 확인해 보았다.
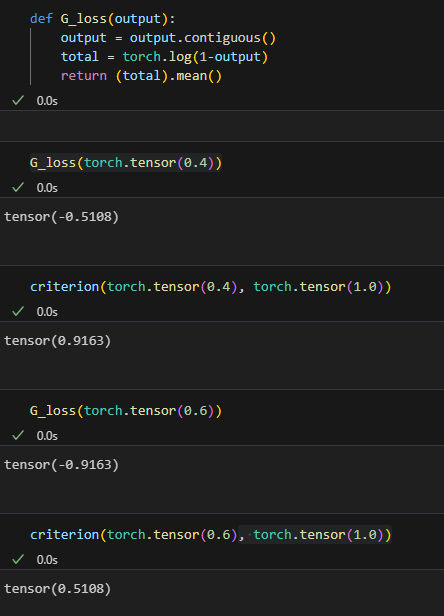
확률값이 높은게 더 좋은 생성자라는 의미이므로 0.4->0.6으로 수렴시켜야 하는데 논문에 쓰여진 식만 썼을때는 일정 확률 이상일때 gradient가 비정상정으로 커질것이므로 좋은 방법이라 생각되지 않아 학습을 한번 돌려봤다.
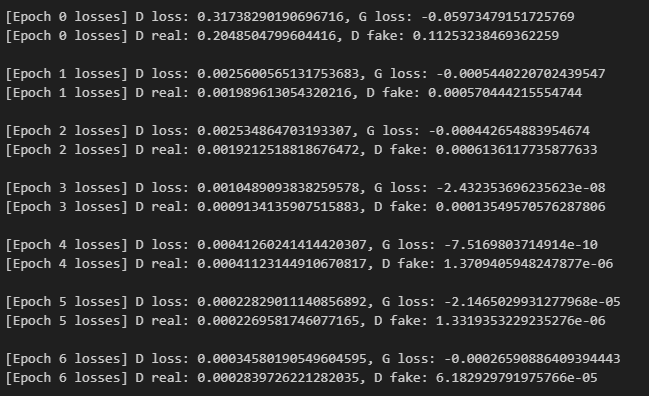
논문에서 이 loss를 사용했을때 G에 비해 D의 성능이 높아 학습 초기에 가중치가 saturate한다고 했으며 실제로 몇번만에 기울기 소실이 일어났다. (D가 G가 생성한것과 data를 너무 쉽게 구분해서)
학습 초기에 기울기 소실 방지를 위해 학습 초기에만 D(G(z))를 사용해 G를 훈련시킨다고 하는데 BCE를 사용하는게 더 안정적이고 구현도 편하고 학습에 지장이 없어서 계속 사용한다고 생각된다.
깃허브 코드 링크: https://github.com/hykhhijk/PaperImplemenataion/blob/master/GAN/GAN.ipynb



